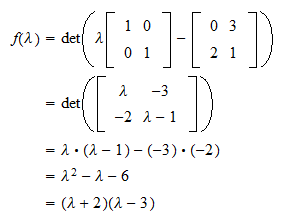Simple Tips About How To Check Linear Independence

2 x + 6 y = 0.

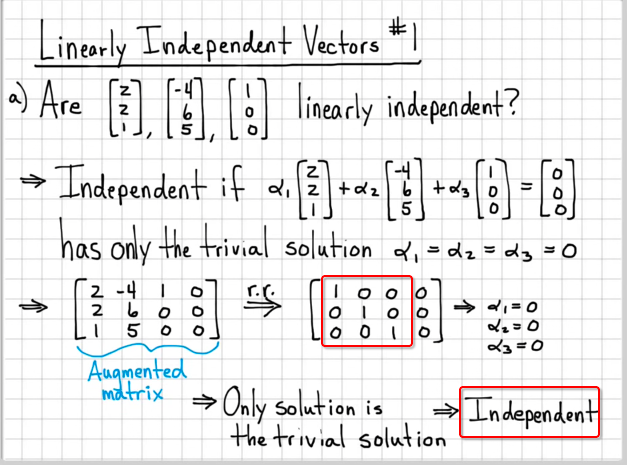
How to check linear independence. | d | = 1 × | 1111 | − ( 1) × |. Finding the solution of the rref matrix. There are three simple ways to check for independence:

In the other direction, if x1v1+x2v2=0with x1a=0(say), then v1=−x2x1v2. If v1=cv2then v1−cv2=0,so {v1,v2}is linearly dependent. X + 3 y = 0.

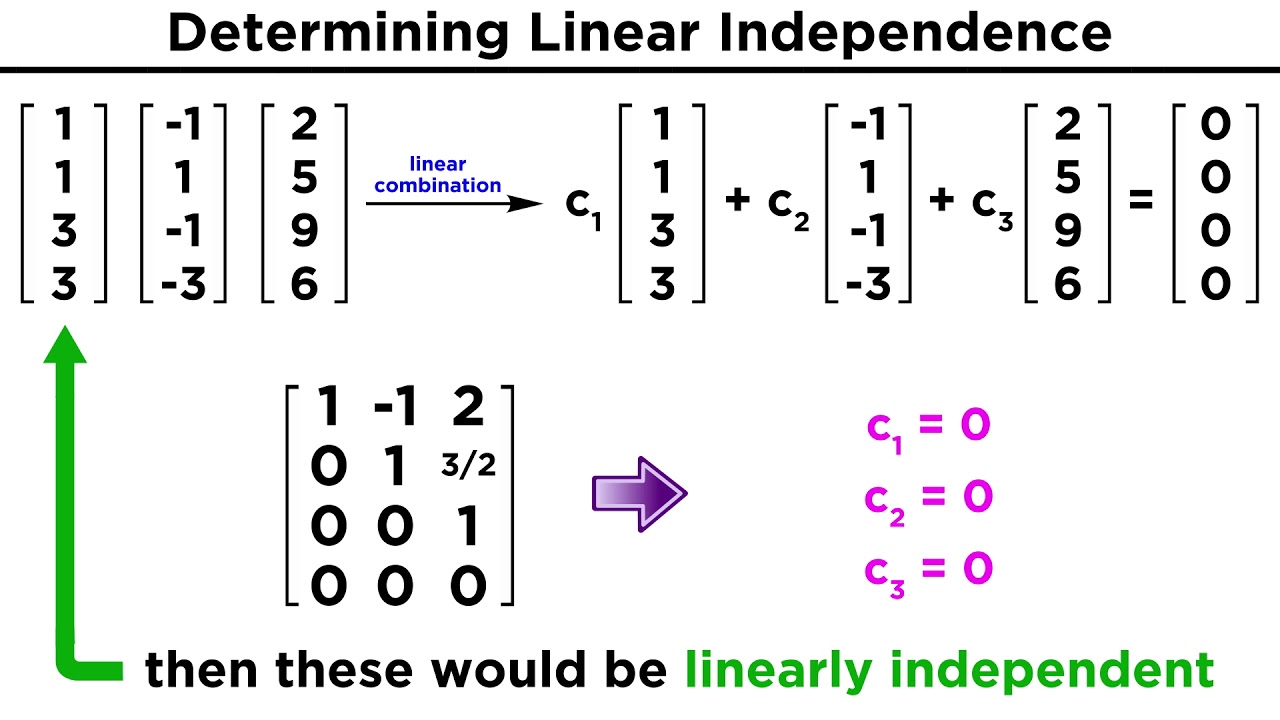
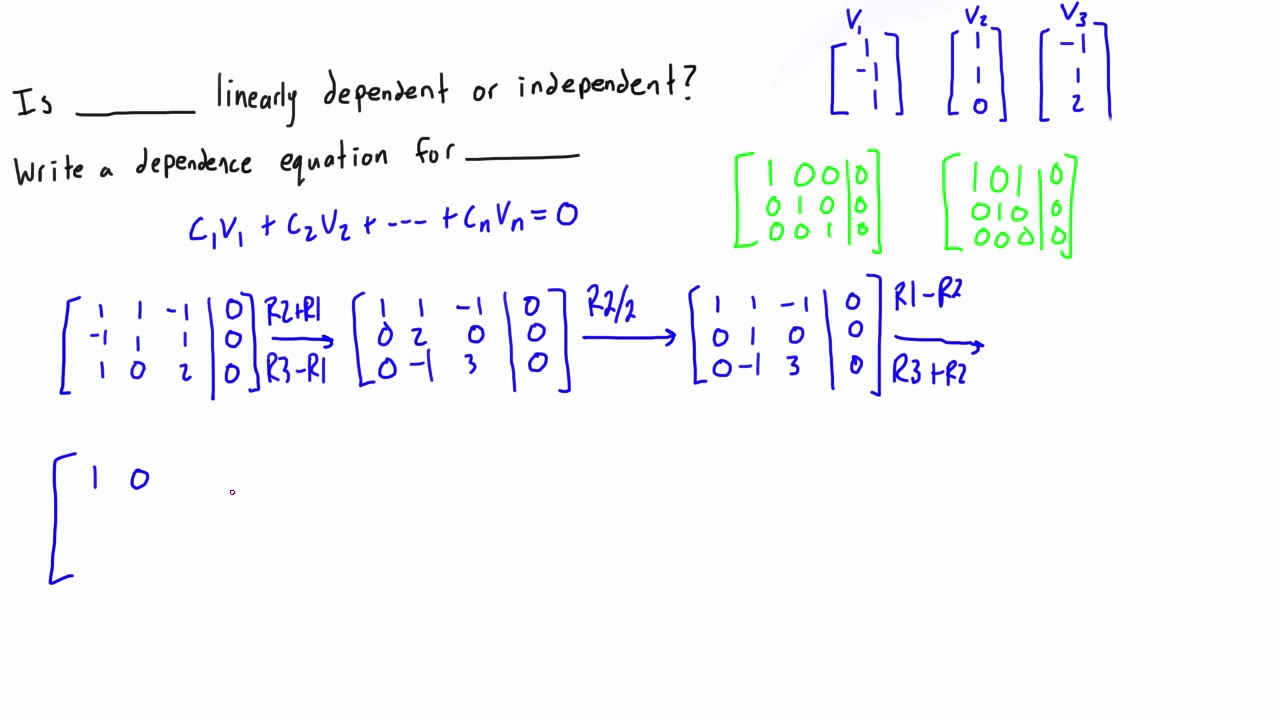
C 1 v → 1 + c 2 v → 2 + ⋯ + c k v → k = 0 →. Check whether the vectors a = {1; Suppose you have the following two equations:

It is easy to produce a linear dependence relation if one vector is. |d|=0, then check for linear independence vectors a, b, c. Simple examples of linear independence test.

Is p (a) × p (b) = p (a and b)? In the other direction, if x1v1+x2v2=0with x1a=0(say), then v1=−x2x1v2. If their determinant is zero.

To find if rows of matrix are linearly independent, we have to check if none of the row vectors (rows represented as individual vectors) is linear combination of other row vectors. How to find out of a set of vectors are linearly independent? A set of vectors is linearly independent if and only if the equation: